Dans le précédent épisode, nous nous étions focalisés sur la description des approches lagrangienne et eulérienne : deux méthodes essentielles afin de décrire le mouvement d’une particule fluide dans un écoulement.
D’ailleurs, toute cette histoire avait justement commencé en définissant ce qu’était une particule fluide, un concept subtil et intéressant qui est propre à cet état de la matière. Ainsi, contrairement à la notion de point matériel en mécanique du solide, la particule fluide peut se déformer en étant soumise à un champ de vitesse non-uniforme. Elle possède donc une surface et un volume infiniment petits : elle est de taille infinitésimale.
Le plus dur étant déjà fait, nous tenterons dans ce nouvel article, de décrire quelques concepts supplémentaires de la cinématique : comment caractériser un écoulement sans avoir besoin de connaître les forces qui lui sont appliquées et quels autres éléments pourraient nous aider à décrire le mouvement d’une particule fluide ?
C’est ce que je vous propose d’explorer aujourd’hui !
La particule fluide en mouvement : trajectoires et lignes de courant
La trajectoire : définition
Vous l’avez maintenant bien compris, la description lagrangienne permet de décrire et de suivre une particule fluide tout au long de son mouvement. Ses coordonnées spatiales sont donc des fonctions du temps car elles se déplacent avec la particule, on les note x(t) et y(t).
C’est donc tout naturellement que cette méthode permet de définir ce qu’est une trajectoire.
Intuitivement, on la comprend comme étant l’ensemble des positions successives prises par une particule fluide au cours du temps. Avec la méthode lagrangienne, il s’agit simplement de ses coordonnées !
Pour plus de précision, il peut être utile de mentionner les positions d’origine de la particule notées $$(x_0;y_0)$$.
Comment l’observer expérimentalement ?
Au-delà d’un tableau de TD, la trajectoire peut se concevoir matériellement et se visualiser en laboratoire.

Rien de sorcier, il suffit de disposer un traceur passif dans un écoulement (des particules réfléchissantes comme le mica par exemple) et de prendre des clichés photographiques avec des temps de pause suffisamment longs.
Le mouvement d’une particule fluide est donc associé au déplacement du traceur attaché à celle-ci. Ainsi, ses positions successives dessinent une ligne clairement identifiable à l’aide du traceur.
Un peu comme un canard en plastique flottant à la surface de son bain, la trajectoire est suivie à l’aide d’un traceur matériel.

Et les lignes de courant ?
Contrairement aux trajectoires qui se déterminent au cours du temps, les lignes de courant se mesure à un instant t donné.
Une ligne de courant correspond à une courbe qui est tangente en tout point au vecteur vitesse de chaque particule fluide. Elles se comprennent comme étant un concept davantage eulérien car elles ne sont pas propres à une seule particule fluide unique mais sont plutôt associées à un champ de vitesse dit champ eulérien des vitesses.
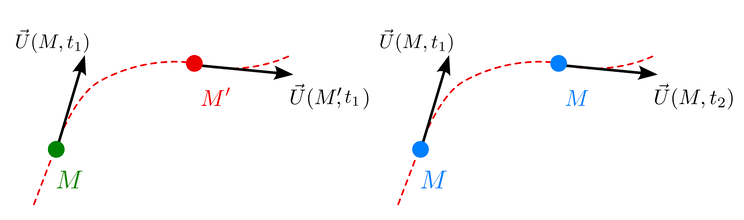
Si on suppose un déplacement infinitésimal de valeur (dx,dy,dz) alors l’équation d’une ligne de courant s’écrit :
$$\frac{dx}{u(x,y,z,t)}=\frac{dy}{v(x,y,z,t)}=\frac{dz}{w(x,y,z,t)}$$
J’insiste ! Ici, t est bel et bien considéré comme étant fixé dans cette définition !
Observation expérimentale
Un peu comme les trajectoires, les lignes de courant se visualisent à l’aide de traceurs passifs introduits dans l’écoulement. Cette fois-ci, il est nécessaire de prendre des clichés photographiques avec des temps de pause courts : on parle alors de caméra ultra-rapide.
À intervalles de temps très petits, le déplacement d’une particule fluide x apparaît comme un petit baton de longueur proportionnelle à la vitesse v(x,t).
La ligne de courant est donc tangente en tout point à ces petites droites qui se visualisent à nouveau grâce au traceur.
Vous sentez l’arnaque ? Pourtant une ligne de courant se mesure à t fixé : comment la visualiser alors au cours du temps ?
Eh bien, dans la majorité des cas ce n’est pas une visualisation directe. Si l’écoulement est stationnaire, tout va bien car trajectoires et lignes de courant sont confondues : pas de difficulté.
Par contre, si ça n’est plus le cas, il faut alors procéder indirectement en mesurant le champ de vitesse instantané puis reconstruire a posteriori les lignes qui sont tangentes aux vecteurs de vitesse.
Cette méthode expérimentale est appelée PIV (Particle Image Velocimetry).

L’écoulement incompressible et la fonction de courant
Qu’est ce qu’un écoulement incompressible ?
Dans l’article précédent, nous avions traité quelques cas intéressants illustrant la déformation d’une particule fluide dans des champs de vitesse non-uniformes.
Les phénomènes de rotation ainsi que d’élongation-contraction ont permis de montrer que le tenseur gradient de vitesse était pertinent pour comprendre les modification subies par la particule.
En particulier, le cas d’une déformation de type élongation-contraction est assez pratique afin d’illustrer une hypothèse utile de certains fluides : l’incompressibilité.
Pour bien la comprendre, commençons par rappeler que pour cette situation, nous avions explicité l’expression d’une composante particulière de la déformation appelée déformation linéaire : \[s_{xx} = \left(\frac{\partial u}{\partial x}\right); s_{yy} = \left(\frac{\partial v}{\partial y}\right)\]
Ces quantités sont cruciales afin de bien comprendre la variation du volume dV d’une particule fluide au cours d’une déformation.
Pour simplifier les choses, supposons une particule de forme rectangulaire. L’application d’un raisonnement plan (2D) permet d’écrire le changement de volume comme suit :
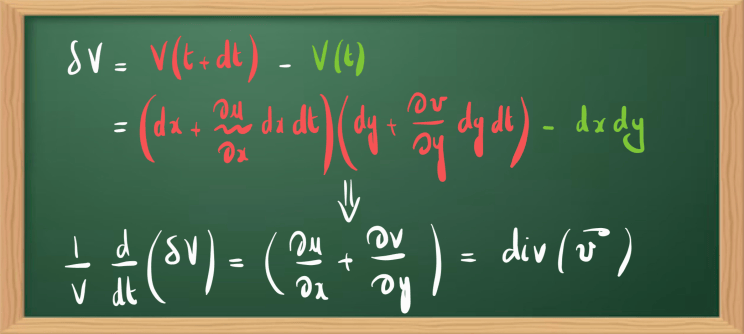
Si vous ne comprenez toujours pas d’où ça vient, je vous conseille vivement de revoir les figures illustrées dans mon précédent article. Il s’agit simplement de prendre la différence du volume avant et après déformation.
Ici, on triche un peu car il s’agit davantage d’une surface plutôt que d’un volume (disons un volume par unité de longueur 😉). Mais ce que l’on constate, c’est que si le volume ne change pas au cours du temps (variation dV = 0) alors la divergence du champ de vecteur est nulle ! C’est bien la définition de la condition d’incompressibilité : les particules fluides ne peuvent ni se contracter ni se dilater !
Cette hypothèse s’applique essentiellement si l’on suppose une masse volumique constante.
En réalité, il aurait plutôt fallu l’appeler hypothèse isochore (car c’est une transformation à volume constant) mais sans doute que le terme incompressible a été utilisé car les liquides sont naturellement faiblement compressibles.
Autre remarque importante concernant le tenseur gradient de vitesse : on notera que sa trace (c’est-à-dire la somme de ses éléments diagonaux) correspond à la divergence du champ de vitesse et donc à la variation du volume !
Voilà une jolie information pour briller en soirée !
Qu’est ce qu’une fonction de courant ?
En plus de vous permettre de frimer face à vos collègues, cette hypothèse permet également de justifier l’introduction d’une nouvelle notion : la fonction de courant.
Vu son nom, vous vous doutez bien qu’elle est un peu liée aux lignes de courant évoquées plus tôt.
Eh bien vous avez raison, car les lignes de courant correspondent justement à des courbes pour lesquelles la fonction de courant est constante.
🧐 Mais d’où vient-elle ?
Mathématiquement, on peut montrer que si la divergence d’un vecteur est nulle alors il peut s’écrire comme le rotationnel d’un autre champ vectoriel. Dans notre cas, on peut appliquer ce résultat sur un champ de vitesse pour un écoulement incompressible :
$$div(\vec{v}) = 0 \Rightarrow \vec{v} = \vec{\nabla} \wedge \vec{A}$$
On dit que le champ de vitesse est solénoïdal et on appelle le vecteur A, un potentiel vecteur.
Dans le cas particulier d’un écoulement plan, il n’y a aucune dépendance à la coordonnée z et on aura donc :
$$\begin{pmatrix}v_x \ v_y \end{pmatrix} = \begin{pmatrix} \displaystyle\frac{\partial A_z}{\partial y} \ -\displaystyle\frac{\partial A_z}{\partial x} \end{pmatrix}$$
En physique, on écrit généralement que la composante Az = ψ : c’est la notation de la fonction de courant.
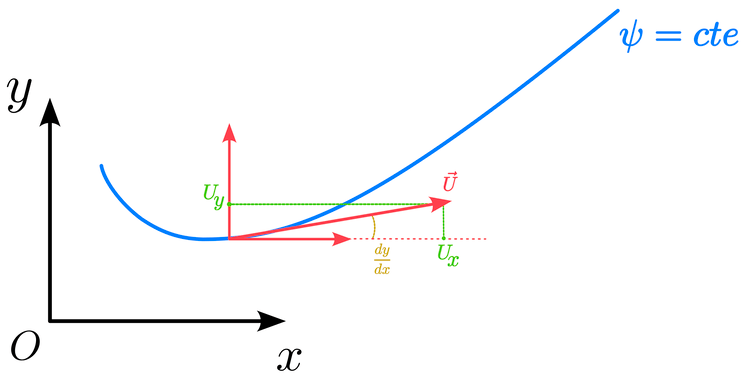
Prenons maintenant une ligne de courant avec ψ = cte, on a alors dψ = 0 :
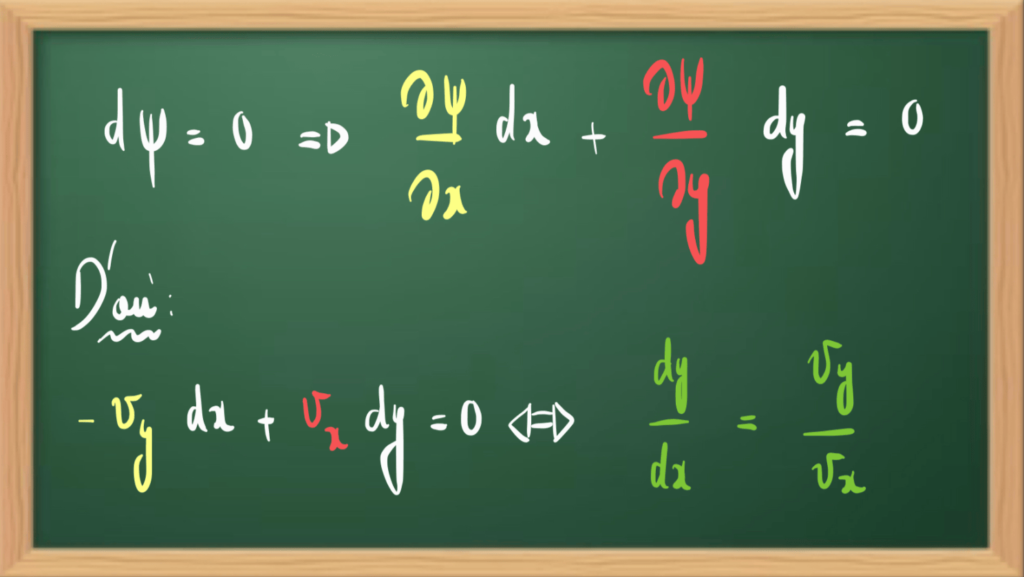
Autrement dit, le champ de vitesse est tangent à la ligne de courant comme souligné précédemment. Ceci est dû au fait que la pente de la ligne de courant correspond à la pente du vecteur vitesse.
Mais la fonction de courant ψ est bien plus pratique que ça. En plus de décrire simplement les lignes de courant (déjà essentielles pour visualiser un écoulement), cette quantité permet aussi de simplifier les équation de Navier-Stokes en supprimant la pression.
En effet, on sait que le rotationnel du gradient d’un scalaire est nul. On peut donc caractériser l’écoulement uniquement à l’aide de la variable ψ ce qui est bien utile pour confirmer rapidement une intuition physique !
L’écoulement irrotationnel et les équipotentielles
Vous le savez à présent, les physiciens adorent se simplifier la vie ! C’est bien pour cela qu’ils utilisent toutes ces hypothèses sur les écoulements : incompressible, lignes de courant, bi-dimensionnel, stationnaire… Vous commencez à maitriser les bases de la cinématique.
Mais il reste une hypothèse laissée de côté pour le moment : l’irrotationnalité. Oui, car les écoulements peuvent aussi être irrotationnels et cela implique justement que… le rotationnel du champ de vitesse est nul. Pas trop avancé n’est ce pas ?
🧐 Alors, qu’est ce que cela signifie concrètement ?
En physique, le rotationnel décrit la tendance d’un champ à tourner sur lui même. Cela est d’ailleurs décrit sous un nom encore plus explicite en mécanique des fluides, car on parle de vecteur tourbillon ou de vorticité.
Cette notion désigne donc la capacité d’une particule fluide à avoir une rotation intrinsèque.
Ainsi, tout naïvement, l’absence de vorticité implique l’absence de rotation : c’est la définition de l’écoulement irrotationnel. Les particules fluides peuvent se déplacer mais ne tournent pas sur elles-mêmes.
Mathématiquement, si le rotationnel d’un champ vectoriel est nul alors on peut écrire ce vecteur sous la forme du gradient d’un scalaire. Pour un champ de vitesse par exemple, on a donc :
$$\vec{rot}(\vec{v}) = \vec{0} \Rightarrow \vec{v} = \vec{\nabla}\phi $$
La quantité ϕ est appelée potentiel des vitesses et elle permet de caractériser des lignes dites équipotentielles pour lesquelles ϕ = cte.
En pratique
Toutes ces notions paraissent assez théoriques mais elles ont bien une utilité pratique !
Dans un écoulement incompressible, la divergence du champ de vitesse est nulle. Mathématiquement, la divergence du gradient d’un scalaire correspond à l’opérateur laplacien.
Dans le cas de l’écoulement irrotationnel où l’on peut écrire v = ∇ϕ, l’application de la divergence à cette expression permet de montrer que la quantité ϕ vérifie l’équation de Laplace. Autrement dit, on a : Δϕ = 0.
Connaître la fonction ϕ permet donc de déterminer directement le champ de vitesse sans avoir à résoudre de longues équations.
Visuellement, les équipotentielles peuvent même aider à se représenter l’écoulement. En effet, il se trouve que la distance entre deux lignes équipotentielles est inversement proportionnelle à la vitesse. Résultat ? Plus les équipotentielles sont proches, plus la vitesse est grande !
On peut même aller plus loin car, pour un écoulement stationnaire, la vitesse est liée à la pression par le biais du théorème de Bernoulli. Connaître les lignes de potentiel signifie que l’on peut donc déduire aussi une cartographie de la pression ! Bien pratique !
Conclusion
La cinématique des fluides semble à la fois intuitive et complexe. J’espère vous avoir donné quelques pistes utiles pour bien commencer à l’étudier et l’appréhender.
À bien des égards, elle constitue, avec la statique des fluides, le socle le plus fondamental de la dynamique des fluides.
Notre petit périple commença avec les descriptions lagrangienne et eulérienne et nous mena jusqu’à l’introduction des concepts utiles de lignes de courant et d’équipotentielles en passant par la redécouverte du tenseur gradient des vitesses crucial pour comprendre la déformation d’une particule fluide.
Notre aventure cinématique s’achèvera dans un prochain court article dans lequel nous tenterons d’exposer une utilité supplémentaire des fonctions de courant dans la description d’un écoulement !